Érdekes módon, egy problematika az elsődleges ráismerést kővetően, inkubációs időperiódusába lép, bensőségesen lappang. Folyamatos készenléti készséggel (fogékonyság), hasonló helyzetek felismerésével, összehasonlításával, beillesztésével, időszakos alkalmi módban folyik a további tematikai adatgyűjtés. Mígnem, az egész logikai adattár el nem éri, modern kifejezéssel élve, a „kritikus mennyiséget” és kreatív alkotó cselekvésre nem késztet. Módszertanos receptről nem beszélhetek, de valahol ebben az irányban kell keresgélni az újítások tevékenységét: egy már létező különféle összetételű (komplex) tudásból és a környezetből, egy közös eredményezésként felismert új összefüggés kidolgozása.
1.) Előzmények és szituáció-felvételezés:
A „Szerszámgépek”, a „Szerszámgépek automatizálása” és a „Gépi megmunkálás forgácsolással”, tananyagilag összefüggőek és igen testhezállóak voltak számomra az Újvidéki Egyetem Műszaki Karának végzős évfolyamain. Kitűnő előadóim voltak, mint pl. Dr. Rekecki József (ma nyugalmazott egyetemi tanár) és Dr. Radoje Milikić (ma a Gépészeti kar igazgatója), úgyszintén kiemelkedő tanársegédek, mint Mr. Hodolič Janko (ma már Dr. és professzor, prodekán).
Fotó 1.: Az újvidéki Műszaki Kar az Egyetemista tér felől, 2006 szeptemberében
(fotó LáVa)
Kitűnőre vizsgáztam, viszont bosszantott, szöget ütött a fejembe, az, hogy egy a könnyűkategóriába eső vizsgapéldát nem voltam képes végig megoldani. Gimnazista létemre, matematikából, fizikából, ábrázoló mértanból tetemes tudás-rajtelőnyöm származott a Műszaki Kar gépészeti szakán, azonban hiányzott egy apróság. A középiskolában nem sajátítottam el a logár léc használatát, mint a gépésztechnikusok. Nem is kellet, már a „
kalkulátoros generációhoz“ tartoztam. Ezért, nem ismervén a logaritmusos számskáláin, az egyszerű műveleteken túli összefüggéseket, az egyenletek megközelítő megoldásaihoz (+/-3% pontossággal), a példa befejezetlen maradt, vagyis számalakú végeredmény nélkül. Megálltam a fordulat áttételi szám kifejezésének levezetését követően, a
K=a/b*c/d –nél, ahol összetevői: K számított racionális szám (pozitív tartományából, bármely decimális tört), az {a, b, c, d} tagok számjegyei pedig a természetes számok {N} készlet halmazából választottak. És, vázlatos rajz nélkül nem lehet tovább értelemszerűen dolgozni! A gépészetben (is), ez aranyszabály. A „levegőben-szórajzok“ szappanbuborékok, felelősséghiányosak és többértelműek.
A megemlített könnyűkategóriás vizsgapélda:
Egyetemes marógépen forgácsolással szükséges kialakítani két (z=2) bekezdéses modul menetet (csigafogazás) ø50mm átmérőjű hengeres munkadarabon, osztóberendezés használatával. Határozd meg a:
a.) Cserefogaskerekeket, azzal a feltétellel, hogy a menetemelkedés eltérései +/-0,005 milliméter keretek között maradjon.
b.) Elkészíteni a művelet teljes képű vázlatos rajzát a megfelelő elemek megjelölésével.
Ismert adatok:
m
n = 2,25 mm ; ferde fogazat normál modulja
S
V = 5/1” ; marógép munkaasztalának menetorsó emelkedése
1/Z= 1/40 ; csigafogaskerék pár áttétele
Cserefogaskerekek készlete: 24, 28, 30, 32, 39, 40, 44, 47, 48, 56, 64, 68, 72, 76, 86, 96 és 100 (fogazatok száma Zi ).
Példa pontszámértéke: 30/100.
Megoldás:
Nyilvánvaló, a b.) ponttal szükséges kezdeni (lásd Ábra 1.), melyre a megoldás folyamata közben áttekintéssel támaszkodni lehet.
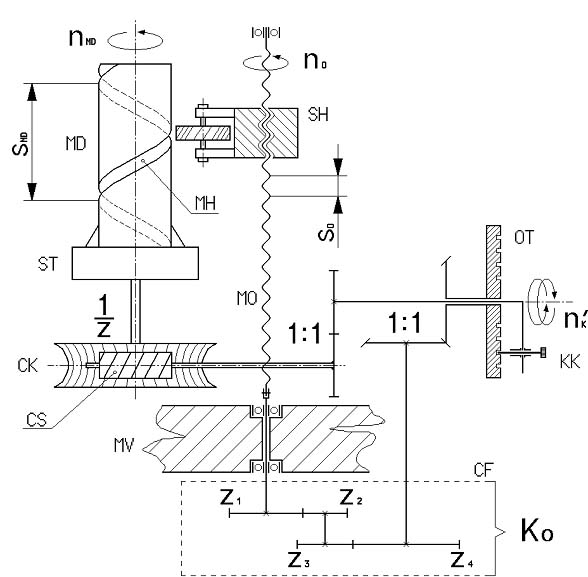Ábra 1. : Egyetemes marógép áttételének kinematikai vázlata differenciálosztású (relatív) osztószerkezettel, ahol
MD – munkadarab
nMD – munkadarab fordulatszáma
MH – modul horony (csigafogazás)
SMD – modul horony emelkedése
ST – szorító tokmány
CS – csiga
CK – csigakerék
1/Z = 1/40 – csigafogaskerék pár áttétele
MV – marógép tartó vázszerkezete
MO – előtolás menetorsója
SO – menetorsó emelkedése
nO – menetorsó fordulatszáma
SH – forgácsoló szerszám hordozója
CF - cserefogaskerekek
Z1, Z2, Z3, Z4 – az áttétel fogaskerekei, megfelelő Z(i)∈{N} fogszámmal
Ko – feladattól függően kiszámított és készletből cseré fogaskerekekből megszerkesztett összegezett áttételi szám, ahol K0∈{R}
1:1 – azonos áttétel (a fordulatszám se nem fokozódik, se nem csökken)
OT – osztótárcsa, mely visszahatóan rá-, vagy elfordulva is segíti a körosztás egészszámúságát (furatai készletével)
KK – kézzel pozícionálható kar
nK – kézzel végzet, osztó fordulatszám
(vázlat: LáVa)
Mindez így hűen a porondra helyezve, talán a komplikált benyomását is keltheti, ami nem volt célom, ezért megpróbálom minél előbb kiszűrni az újítás lényegét, ami már egy tréningben lévő gépészmérnökhöz képest, különösebb előtudás nélkül is értelmezhető.
Az a.) pont megoldáslépései:
S
O = 5/1” = 25,4/5 = 5,08mm ………..……………………...(1)
A munkadarab (MD) modulhorony (MH) emelkedésének sebessége azonos a menetorsóéval (MO), vagyis ezzel a szerszámhordozóéval (SH), tehát:
n
MD* S
MD = n
O* S
O ………………………………………....(2)
Mivel a kinematikai összefüggés a munkadarab (MD) egy (1) fordulatán belül jön létre (így tervezzük, alapfeltétel, különben a szerszám és stb. koliziójára kerül sor = egymásba hatoló törés)
1/ n
O = S
O/ S
MD = K = Z
1/ Z
2* Z
3/ Z
4*1/Z = K0*1/Z …........(3)
Innen adódik:
K
0 = (S
O*Z)/ S
MD = 40* S
O/ S
MD ……………………………(4)
Ki kell számítani a munkadarab emelkedését (a példában ez volt az eredmény elérésébe betervezett közvetett mód, a szokásos „kétlépéses” megoldás):
S
MD = (m
n*π*z)/cosβ ………..……………………………(5)
ahol: z = 2 ; a bekezdések száma
β = ?
Legegyszerűbb módja, ha kiterítsük a módul menetcsavarulatát egy síkba:
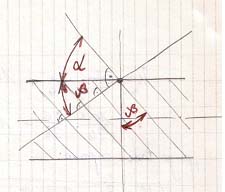Ábra 2. :
A kiterített horony modulemelkedése
α – menetemelkedés szöge
β – menet dőlésszöge
(vázlat: LáVa)
Trigonometria összefüggés felállításával kiszámítjuk a β szögértékét:
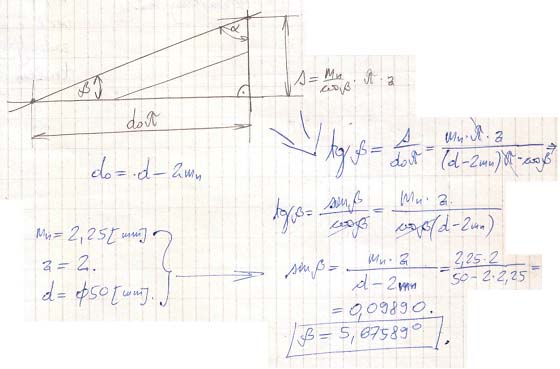Ábra 3. : Eredeti kézirat melléklése (vázlat: LáVa)
A kiszámolt értékek behelyettesítésével következik:
(5) → S
MD = (2,25*3,14*2)/cos(5,67589) = 14,20682mm
Majd:
(4) → K
0 = (5,08/14,20682)*40 = 1430299 = Kközépérték = K
MID
Kiszámítjuk a tűrésmező maximális/minimális határértékeit:
KMIN = 40* S
O/ S
MDmax = 40*5,08/(14,20682+0,005) = 14,29795
KMAX = 40* S
O/ S
MDmin = 40*5,08/(14,20682-0,005) = 14,30802
És most értünk oda, ahol megállt a tudományom a vizsgán:
…………………………………..(6)
Ki kell négy (4) olyan fogaskereket választani a felkínált készletből, amelyek összeillesztésével az Ábra 1. alapján, elérjük a szükséges kiszámolt K0 áttételi számot.
Ki kell négy (4) olyan fogaskereket választani a felkínált készletből, amelyek összeillesztésével az Ábra 1. alapján, elérjük a szükséges kiszámolt K
0 áttételi számot.
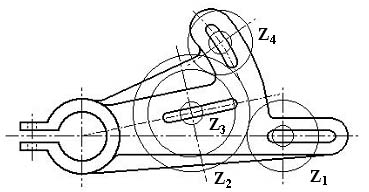Ábra 4. :
A cserefogaskerekek Z1, Z2, Z3, Z4 szerelhetősége a tartó villára
(vázlat: LáVa)
Tisztán matematikai szempontból szemlélve a problematikát, most már megtehetjük, a képlet egyszerűnek tűnik: két osztás, egy szorzás!? Ez is valami, ezen a szinten?
Ne feledkezünk meg a számjegyek adott és megkövetelt természetéről, ami a beszámoló elején elhangzott már:
K
0∈ {R} ; Az áttételi szám csak kivételesen ritkán egész szám, óriási többségében tört számot képez. Mindkét eset összefoglalható a racionális számok halmazával R(i)
Z
(i)∈{N} ; Egy fogaskerék fogszáma mindig egész természetes N(i) szám!
Tehát, a rendelkezésre álló természetes számok Z
(i) kombinálásával kell eredményként megkapni a K0 számot, úgy hogy a tűrésmezőbe essen:
Lehet próbálkozni, a mosoly, ha volt is, gyorsan elmarad, nagy valószínűséggel fagyni fog.
2.) További szembesülések a gyakorlatban:
Nyári kötelező gyakorlataimat a „Potisje” Ada szerszámgépgyárban végeztem, három – három hetet az első, második és harmadik évfolyamot követően. Itt találkoztam újból a leírt vizsgaproblematikámmal is.
Nem kis meglepetésemre a felállított matematikai problematikára nem volt egyértelmű megoldás. Mindenki használta a saját kis megoldásmodell felépítményeit, amelyek működtek, vagy nem (becenevükön „lottószisztémák”). Úgyszintén, minden gépgyártó mellékelte, vagy nem, a többrészes könyvszerű táblázatokat gépe mellé, ahol a szabványosabb áttételi számok K0 elérése természetes számú fogazattal, adva volt a közismert Logaritmus táblázat könyvecske módban: több száz oldal teli csupa számokkal.
De, a termelésben sűrűn előfordultak nem szabványosak, a gyártott univerzális és speciális gépek fejlesztése folyamatos volt és fogadtak kooperációs alkatrészeket is. Ilyenkor, havonta akár többször is, a fogaskerék-technológusok akár egész munkaidejük alatt is (n x 8óra hossza) „alsóst játszottak” osztással és szorzással. Keresték az egyetemes esztergapadokhoz, vagy marógépekhez, a fogmarókhoz és fogköszörűkhöz az áttételi számot. Előfordult, hogy fogaskereket gyártattak a már létező készlethez, mert pont egy olyan természetes számú kombinációra akadtak, amelyhez nem voltak ki a fogaskerekek. Áttekinthetőség a megoldás(ok) mezején nulla – zéró – szintű volt.
A termelékenység görbéje ebben a műveletpontban nem mélyrepült, hanem lezuhant.
Fotó 2. : Az adai „Potisje” szerszámgépgyár serelőcsarnoka a kilencvenes évek elején
(fotó Király János)
…Folytatása következik…
.jpg)
