Fogazatos ötletelés, avagy K=f(N)

1. rész

Öt (5) tényező kellet összességében az újítás prototípusának kidolgozásához. Ezek a következők:
1.) Téma felismerése
2.) Létező igény
3.) Megoldás törvényességének megfejtése, a kulcs
4.) Működő prototípus és
5.) Tesztelése valós környezetben

Az első kettőről (1. és 2.) beszámoltam az előző, „Fogazatos ötletelés” 1. részében. Most folytatjuk, előszörre is egy kis alkotó filozofikus résszel (első olvasáskor nem kötelező a 3.1. rész, bár később valószínű, visszatérők leszünk):

3.1.) A logikai adattár elérte a „kritikus aktív mennyiséget”:

Munkába állva, gyakornokként minden hónapomat más, más munkakörben töltöttem el. Intenzíven lekötötte figyelmemet a gyár, a láncszerűen egymásba kapcsolódó termelési folyamataok részletesebb megismerése. Hűen fejleszthettem és bizonyíthattam akkor is, és ma is, hangoztatott állításomat: elmélet és gyakorlat között nem lehet különbség. Ha van, akkor vagy az egyik, vagy a másik a nem jó (Ezzel azonnal belevágtam a közepébe, az érdekviszonyokba, elvágva az örökösen meddő munkás - mérnök „ki a fontosabb” vitát. Mindkettő nagyon fontos, színvonalasan! Figyelem: nem jár érte köszönet, csak eredményesség a „sok lúd, disznót nem győz” eseteknél.)

Ez az állapotokra érvényes. Változtatásoknál pedig, úgyszintén, vagy az egyik, vagy főleg a másik az előreszökkenő húzóerő, és összefüggő párjával, szakértelemmel le kell követni, csapatszerű összeműködéssel.

Természetesen, univerzális recept itt sem létezik, de aranyszabály az előre haladó – fejlődő rendszereknél (Műszaki egyetem, tantárgy: „Termelési rendszerek és irányításuk”), az értelemszerű gazdaságossági tényező: a legnagyobb nyereség, a legkisebb veszteségekkel érhető el. Ha végigmegyünk először egy termelési rendszeren, bár három (3) észrevételünk is megfogalmazódik, mit kellene és hogyan másképpen csinálni. A kitűzött cél kritériumának ABC analízis sorrendje adja meg, legcélszerűbben, egy irányítható rendszeren belül a legaktuálisabb témákat. Természetesen képzetség és hitelesség kell hozzá, ezért jegyzeteljünk. Lassan érjünk messzire.

Nem volt lehetőségem a munkaidőm belül foglalkozni a fogazatos témámmal. Szabadidőmben, különösebb eszközök nélkül, papírral és ceruzával fejtegettem a jelenség szabályait. Meg akartam érinteni a matematikai törvényességét, a cserefogaskerekek által elérhető összes áttételi szám mezőjét {K₀}, amelybe „csak odanyúlnák” és azonnal megvan a megoldás, vagy mindjárt kitudódna, hogy az nem elérhető ebből a készletből.

Ehhez használtam a Matematika indukciót, egy csodálatos eszközt, amelytől „leeset az állam” megismerése alkalmával, végre egy teremtő matematikai eszköz: jelenségek sorozatából felismerni a függvényszerű törvényességet, „kiugrasztani a nyula(ka)t a bokorból”! Végre választ is kaptam az egy ideje bennem vízhangozó kérdésre: „Mi is a függvények értelme a gyakorlatban?” A jelenségek összefüggéseinek leírása, akár a természettudományokban, akár társadalomtudományilag (ezt neveztem meg: részben logikai pozitivizmusnak). Erre már csak a függvény meghatározása mért pontokon keresztül (hosszméret, tömeg, hőmérséklet, feszültség, stb.) tett rá számomra hasonlót, azaz diszkrét jelenségekből (ponthalmazból) analóg (folyamatos) függvényt alkotni. Ezáltal ismerté, vezérelhetővé válik (a paramétereken – mutatószámokon keresztül), és betekintést nyújthat folyamatán keresztül a közel múltba (kontrollként) és a közeljövőbe is (elvárhatóságok, modernül „trend tölcsére”). De, ez egy másik igen érdekes téma.

Visszatérve a kiválasztott konkrét témához:

3.2.) A megoldás kulcsa

Egyszerű példából kiindulva, feltételezzük hogy a váltófogaskerék készlet csak n=5 fogaskerékből tevődik össze, a Z₁, Z₂, Z₃, Z₄ és Z₅–ból. A fogak számértékére most nem helyezünk hangsúlyt, mert a váltakozás törvényességét figyeljük meg, ebben az egyszerű alsós matematikai kifejezésben (az első részben a 6. egyenlet):
K₀ = Z₁/Z₂ * Z₃/Z₄ ...............(6)

Ahol a Z₁, Z₂, Z₃ és Z₄ a cserefogaskerekek felszerelhető helyét jelölik meg. Tehát, nem fogszámokat, hanem helyhez kötött indexes változókat jelképeznek, amelyeken rendszerbefoglalt sorrendben váltakoznak a fogszámok a készletből (lásd Ábra 4. az első részből).

Honnan érdemes kezdeni a fogaskerék rendszerbefoglalt váltakozását?

a.) Képzeljünk el egy járműveken alkalmazott kilométer számlálót, és analógiával felállítjuk a cserefogaskerekek-számlálóját: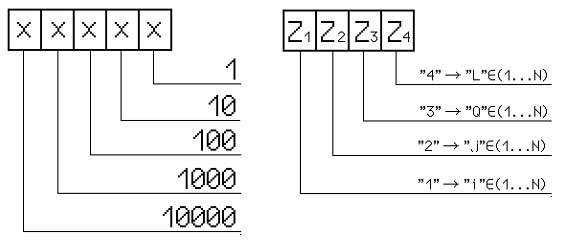


Ábra 5. : A kilométer- és analógiával létrehozott cserefogaskerék-számláló
(vázlat: LáVa)

Ezáltal, új írott alakot vesz fel a kifejezés:
K₀ = Z_i/Z_J * Z_Q/Z_L ...............(6)
Vagy rövidebben leírva, de értelmileg ugyanaz:
K₀ = I/J * Q/L ....................(6a)
Számláló működése: Nem érintve a többi I, J és Q helyet, az L helyen a legkevesebb fogszámtól kezdve és a legtöbb felé haladva váltsuk sorba a cserefogaskerekeket. Mikor ez végére ér, a Q –t növeljük a következő Q+1 értékre és megismételjük az előbbi számláló ciklust. Az „L” ciklussal kimerítsük a Q index tartományt, ami a J+1 tartományba vezet. Így lepörgessük az összes lehetséges változatot is, az „i” tartomány utolsó n tagjáig is. Ez a teljes elképzelhető eredmények mezeje EM = 5*5*5*5 = 252 = 625 eredménnyel.
Grafikusan ábrázolva már kezd áttekinthetőséget nyerni a kereset mező: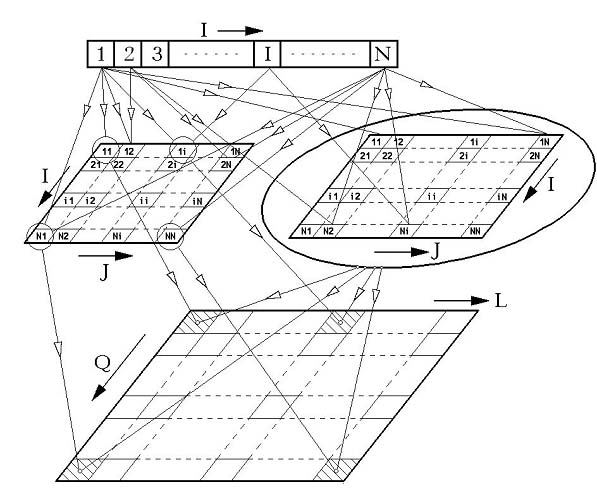


Ábra 6. : A négyindexes I, J, Q, L számlálás lepörgése négy síkban (4S)
(vázlat: LáVa)

b.) Azonban, nem lehet figyelmen kívül hagyni a tagok közti operátorokat, a szorzást és az osztásokat. Itt nem látatlanra húzzuk ki a színes golyókat a dobozból, hanem műveletekkel kötődnek egymáshoz. Ezért, figyelembe kell vennünk a következőt is:
(1/2) * (3/4) = (1*3) / (2*4) = (3*1) / (4*2) = (1/4) * (3/2) , stb.
, mert az egyenlet mindkét oldalán a nevezőben van a 2 és a 4 (és tudjuk hogy 2*4 = 4*2 → kommutáció), a számlálóban pedig az 1 és 3 (úgyszintén 1*3 = 3*1). Ez a matematikai törvénység (kommutáció) megrövidíti az eredmény mezőt a ráduplázásoktól a következő képen: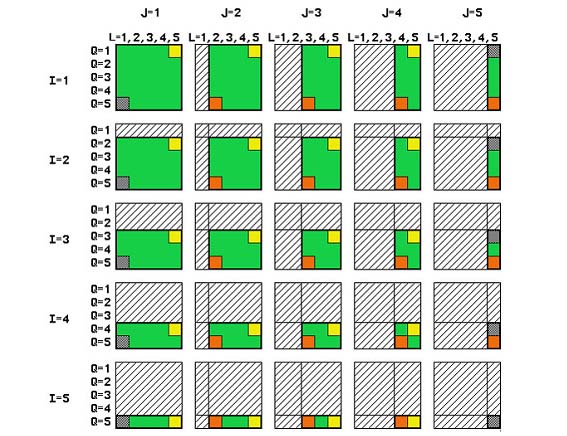



Ábra 7. : A matematika indukció első példalépése jól tükrözi a második indextag (Q/L) szorzandó függőségét az elsőhöz (I/J) képest. Minden I és J számlálóváltásnál rövidül. A használható eredményeket jelképezik a zöld négyzetmezők. (vázlat: LáVa)

A csak egyszer jelentkező eredmények száma ezzel lecsökkent, értéke EM = 225 (a zöld mezőnégyzetek száma).

c.) Figyelembe kell vennünk az is, hogy egy index egyidejűleg csak egyszer jelentkezhet. Ezt diktálja a fogaskerék készlet mivolta: egy fogaskereket egy K₀ megszerkesztésénél a tartó villára, csak egy helyen használhatunk (ismét lásd Ábra 4. az első részben). Ha azonos is lenne két fogaskerék fogszáma, az indexük különböző, ezért egyelőre függetlenül szerepelnek a számlálón. A kizárások matematikai formája:
I: minden értéke használatos, azaz 1..5
J: ha J=I akkor a rákövetkező indexértéket kel használja, azaz J→J+1
Q: ha Q=I vagy Q=J akkor úgyszintén Q→Q+1 és
L: ha L=I vagy L=J vagy L=Q akkor L→L+1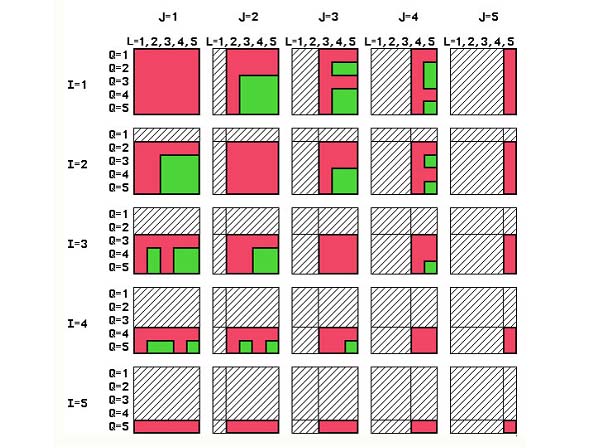


Ábra 8. : Számlálásnál az egyforma indexszámok elkerülésével az első szorzónál (I/J), a megoldás mezeje (zöld) tovább zuhanóan csökkent.
(vázlat: LáVa)

A piros mezők a kiesők, nem szerelhető eredmények. A reális eredménymező zsugorodása most már elérte az EM=50 lehetséges pozitív eredményt.

d.) Mivel a második (Q/L) szorzóban sem lehetnek azonosak az indexek, a megfelelő eredménymező még tovább csökkenthető.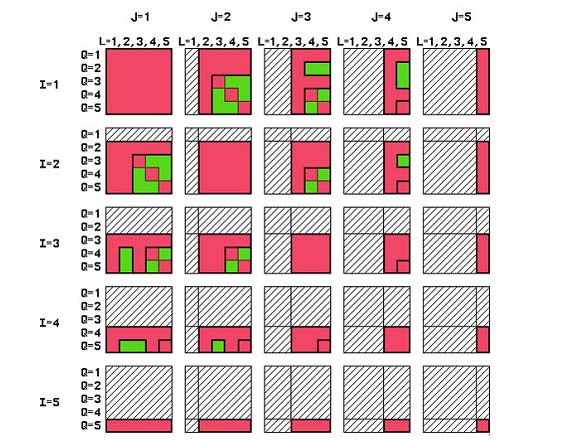


Ábra 9. : Számlálásnál az egyforma indexszámok elkerülésével a második szorzónál (Q/L) is véglegesíti az eredmények mezejét (EM), amelyen egyáltalán lehetséges az igényelt K0 keresése (zöld mezők). (vázlat: LáVa)

A végleges reális eredménymező ezzel elérte az EM=30. A csökkenés a kezdetleges totális módszertan nélküli számláláshoz képest:
EM₀/EM_V = 625/30 = 28,333 szoros(!) , vagyis a kutatandó megoldást esetleg tartalmazó mező a 100% -ról, 4,8% -ra csökkent!

e.) Az összes kombinációk száma, ismétlés nélkül, öt (n=5) elemnél, négyes (k=4) csoportban összefoglalva:
C_n^k = n(n-1)(n-2)…[n-(k+1)]/k = n(n-1)(n-2)…(n-k+1)/k
A kezdetleges példánknál:
C₅⁴ = 5(5-1)(5-2)(5-3)/4 = 5*4*3*2 /4 = 120/4 = 30.
Valóban, ezt az eredmény kaptuk logikai grafikával is!
Ennek ismeretében most már esetleg lett volna esélyem a vizsgapélda befejezéséhez, némi römikártya és/vagy sakklépés irányított szerencséjével, bár a megfelelő K0 eredmények megtalálása ezzel még nem ért vége. A java még ezután következik. Elvégre, itt csak öt (5) elemes cserefogaskerék készletet analizáltunk.

…Folytatása következik…