- Heti Ajánlat
- Természet
- Történelem
- Kultúra
- Nyelvtudomány
- Életmód
- Technika
- Tudósok
- Közélet
- Diákoldal
- Olvasóink küldték
- Tanítástan
- Pszichológia
e-Learning
- Tudta-e?
- Egy élet alatt nagyjából hat elefánt súlyának megfelelő ételt fogyaszt el egy ember.
44. szám - 2008. június 23.
8. részFogazatos ötletelés: továbbra is a programEgy valós gépészmérnöki újítás (innováció) fizimiskája, a „hasznos javaslat” csoportjából, és körülötte:
|
|
1. rész 2. rész 3. rész 4. rész 5. rész 6. rész 7. rész Miért csak a nyolcadolás (1/8) mélységéig vezetettem rá a számlálót a keresett Ko eredményig, tehető fel a természetes kérdés? Miért nem 1/16, 1/32, 1/64, 1/128, stb., a nagyon is ismerősnek tűnő (bitvonalak) részegységekig? Racionális megfontolásból. Ezen alul rövidíteni a keresés „L” index pontvonalát már új, nem biztos, hogy „kifizetődő” (lásd előző 7. rész, utolsó három bekezdését) kísérletezést igényelt volna. Ugyanis, előre ismert modellt véve alapul, a használt kulcsok próbafuttatásai során célmellőzések (átugrások) is jelentkeztek. Megbomlik a természetes egészszámúság {N} a „rövidebb” váltófogaskerék készleteinél, mint például a PA → n=29. Ezért, elfogadtam a „precíz lövedékek” stratégiai elméletéből (a 1960. években megkezdett nyugati országok fejlesztési stratégiája) az elegendő (minimális) közelséget, majd aktiválást: legalább hármas - négyes „sorozat” leadását eredményezi. Érintkezős találat nem mindig jelentkezik (kiváltképpen: most pont azokat kutatjuk, a Ko-kat). Akár egy légvédelmi föld – levegő rakéta. Matematikailag most semmiben sem különböznek a célravezetések. Érdekes ugye? A rakéta előre kihosszabbított tengelyvonalának kitérései a célponthoz képest (mértan), állandó folyamatossággal részekre bontódva eliminálódik, a célravezetőbb részek felé. Mígnem a cél közelébe nem ér. Azért mégis, honnan tudja egy száguldó rakéta, mikor van legközelebb a célhoz? Azt nem tudja, de az első távolságnövekedő jelre: bumm, és vagy talál, vagy nem, de legalább a „célközelben” megpróbálta. Ki gondolta volna, hogy egy nagyüzem sorozatokban előállító fogaskerékvonalán dolgozva, tulajdonképpen egyben „rakétavezető” is lettem. 4.6.2.7.) Célzó alprogram 1. RENDSZER/4 TM-ML: Lássuk akkor az első (1/2) és második felezést (1/4) ábrázoló vázlatot: 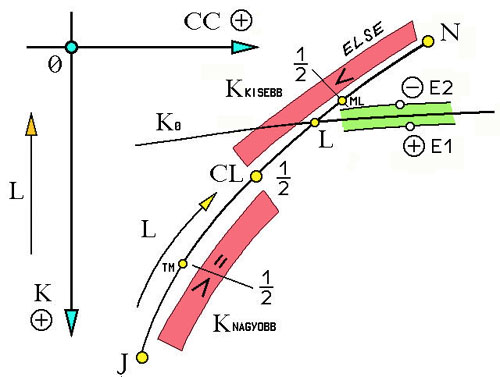 Ábra 26. : Az számláló „L” J-N sárga indexvonalka kétszeri felezésének (1/4) modellje, paraméterek bevezetésével. Rajzolta: LáVa 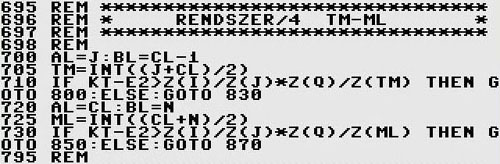 Ábra 27. : A számláló legbelső „L” hurokjából kivezető ELSE elágazásainak alprogramja. Az „L” ciklusonként váltakozó, újonnan megnevezett általános értékhordozó AL és BL határpontokkal. Programozó: LáVa Ugyanezt megfogalmazva kódsorokban, láthatjuk a következő 27. ábrán: A fenti alprogram 700, vagy 720. kódsorára, az új felező kulccsal ugrasztottam ki a program futóvonalát a magból, a már említett mag 457. kódsoráról. A „CL” első felezésének (1/2) középpontját a 456. kódsorában (lásd előző részt) határoztam meg, helyodaillően. Erről az negyedelő (1/4) alprogramról nyílik a következő nyolcadoló (1/8) alprogram: 4.6.2.8.) Célzó alprogram 2. RENDSZER/8 M6-M7-M8-M9: Mindegyik ELSE elágazásnak, a 27. ábra alapján, logikaszerűen két (2) új elágazása van a 28. ábrán. 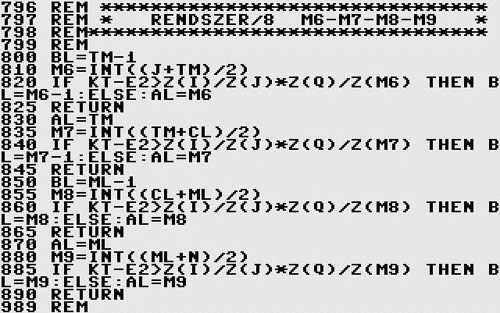 Ábra 28. : Továbbra is a számláló legbelső „L” hurokjából eredő, a negyedelő (1/4) alprogramon át kivezető ELSE elágazásainak újabb, nyolcadoló (1/8) alprogramjai. Programozó: LáVa Kódsorszámokkal kifejezve: 710. → 800. or (angolról: vagy) 830. 730. → 850. or 870. A pontosított 25. (24d.) logikai ábra (lásd 7. részt), amely alapján íródtak a 28. ábra kódsorai, most így fest: 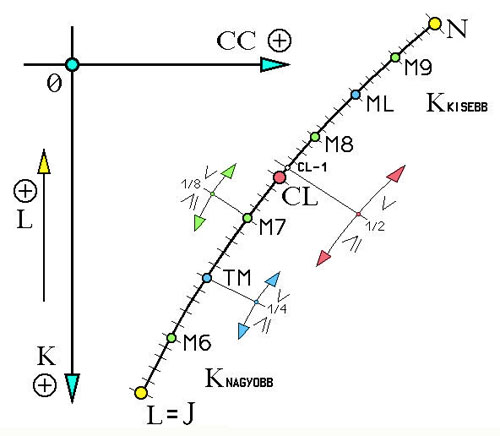 Ábra 29. : : Az számláló „L” J-N sárga indexvonalka nyolcadolásának (1/8) modellje, paraméterek bevezetésével. Programozó: LáVa Elvégezve itt az eredmény Ko esetleg telibe találóan tartalmazó tartomány kiválasztását, RETURN-al visszaugrasztom a programfuttatás vonalát a magba, egy sorral léjebb mint ahonnan indult, névszerit: indult a 457. kódsorról, visszatért a 460. kódsorra és fut (RUN) tovább, most már konkrét értéket számítva az indexek alapján behelyettesített fogszámokkal és ezt a grafikus képernyőre ki is rajzolva. A megváltozott folyamatkövető vizuális külalaki forma kinézete:  Ábra 30. : A képernyőn grafikusan követhető a számlálás folyamata. A vonal képezi a keresett Ko áttételi számot, amelyet „golyószóró” módban indexsorozatokkal átpásztáz a számláló. A ”J”, „L” és „Q” indexpergések jól kivehetők a képernyőről lementett képről (Print Screen). Programozó: LáVa Összevetve a 29. ábrát a 24b. ábrával (lásd 7. részt) a különbség szembeötlő. Nincsenek: hosszan lenyúló „L” indexvonal-sorok, a „Q” harmonikaszerű tömbök többszörösen keskenyebbek, a „J” és főleg az „I” számlálótömbök határai nehezen felismerhetők egy képernyőn belül. Egyszóval, a számítási mező alaposan meg lett „tizedelve”, azaz itt nyolcadolva. A célzások találatai szórásmentésebbek, simulékonyabbak. Nem a Ko vonal átmetszése, hanem lekövetése a módszer. Az Ko eredmények meglepő gyorsasággal és pontossággal pörögnek kifele a számlálódva kutakodó: kulcsolt, szűrt, tartományozott eredményeket rejtő mezőkből. Magyarul: gombnyomásra (a következő részben…). BÖLCSELET: A szegény fiú esete a Királlyal és szemrevaló leányával, akit nagy odaadással és bátorsággal kiszabadított a gonosz elrablói karmai közül, is ide vág. Hogyan? Fordítva mint a mesében: felezősorban, egészen a molekulákig, esetenként atomokig, amelyek még mindig anyagformáló {N} számok. A MESE: Jutalomként, a mesék szerit ilyenkor a Király nagylelkű ajánlata következik. Az összesereglett udvarnép előtt ki is jelentette: „Fiammá fogadlak, odaadom neked királyságom felét és leányom kezét”. Erre azonban, egy meglepetés erejével ható fordulat következett: „Nagyrábecsült, méltóságos Királyom, elfogadom a lányod kezét, hisz szeressük egymást, de a fél királyságod helyett inkább adj nekem annyi búzaszemet, ahány ráfér egy sakktáblára, de úgy, hogy az első mezőre (A1) egy szemet helyeztetsz, minden következőre pedig mindig a dupláját, egészen az utolsó (H8) mezőig”.  Ábra 31. : A Király, a szegény fiú kéz a kézben a királylánnyal és a gonosz elrabló, a 64 sakkmezőn, a mese közepén, még búzaszemek nélkül. Vázlat: FRITZ10 & LáVa Rácsodálkozott a Király magában, nem e együgyű a veje jelöltje, de kiadta a parancsot, hátha így olcsóbban megússza: „Búzát ide…!”. Könnyedén haladt az első mezősor kirakása A1 és H1 között, az emberek mosolyogtak. De már a harmadik sornál (A3-H3) a dolog kezdett érdekessé válni, a mosolyok kezdett ráfagyni az arcokra. Nagyon sokk lett a búzaszemek mennyisége, nem fért a palotaterembe. Se baj, a másik magtárból is hozatott a Király. A végére, kisült, nagy rácsodálkozások közepette, nincs annyi búzaszem a királyságában, meg a világon sem, hogy duplázva elérhető legyen a H8, a 64. mező. A ravasz fiú a Királyt is megleckéztette, és búzaszemgazdagságában dúskálva, új életet kezdetek kedvesével. Azóta is vígan élnek és sok gyerekük született. A Király meg csak elmosolyodik így Péter-Pál felé, az aratás kezdetén, egykori naivitásán és veje éleseszűségén, amiből ő, a nagy Király is tanult. Aki nem hiszi, járjon utána. Itt az aratás ideje, számolhat: (2)64, azaz 2E64=?! …Folytatása következik… |
Kapcsolódó cikkek
- Olvasóink ajánlata

