Fogazatos ötletelés: az algoritmus

4.3.) Az eredménymezőn (EM_V) kutakodó számláló folyamatábrája, az algoritmus: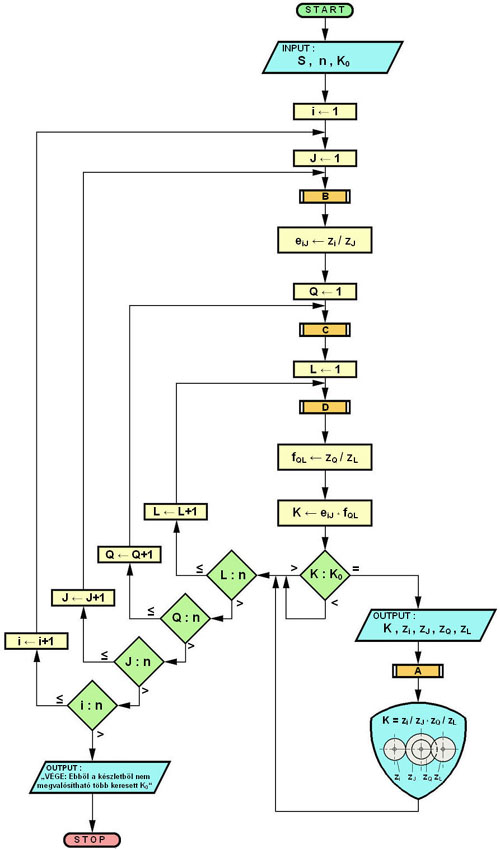


Ábra 15. : Általános algoritmus, megfelelő K:K₀ pozitív racionális áttételi számok {+R} felkutatására, művelet-összefüggő (!) természetes számok adattárából {N}, ahol (sorban olvasva az ábráról):
Vázlat: LáVa


START – kutakodó folyamat (program) elindítása.
INPUT – kezdő paraméterek értékeinek megadására szolgáló interface.
S - szerszámgép meghatározása a felkínált választékból, amelyben az utolsó választás tetszőleges gép is lehet (fogazat számok kézi bevitelét fogja eredményezni). Ezzel adott a váltófogaskerék készlet is, fogszám tételesen (kiolvastatás betáplált adattárból).
n – váltakozó fogaskerekek darabszáma a készletben (nem feltétel mindig mind figyelembe venni, vagy az új készlet kézi bevitele esetén a benne váltakozó fogaskerekek darabszáma).
K₀ – az ismerős, „ki körül forog most a világ”, a kiszámított szükséges áttételi szám, melyet meg kell valósítanunk a váltófogaskerék készletéből (lásd 6. tételt az 1. és 2. részben).
i ← 1 – az „i” indexszámláló felveszi kezdőértékét.
J ← 1 – a „J” indexszámláló felveszi kezdőértékét.
B – eredményszűrő B kritériuma: i ≠ J.
e_iJ = z_i / z_J – az első kettő index pár (i, J) alapján behelyettesített fogszámok hányadosa.
Q ← 1 – a „Q” indexszámláló felveszi kezdőértékét.
C – eredményszűrő C kritériuma: Q ≠ i és Q ≠ J.
L ← 1 – az „L” indexszámláló felveszi kezdőértékét.
D – eredményszűrő D kritériuma: L ≠ i és L ≠ J és L ≠ Q.
f_QL = z_Q / z_L – a második kettő index pár (Q, L) alapján behelyettesített fogszámok hányadosa.
K ← e_iJ * f_QL – folyamatban kiszámított összehasonlításra szolgáló K áttételi szám
K : K₀ – a folyamatértékű K és a keresett K0 áttételi számok összevetése: kisebb, nagyobb, egyenlő.
OUTPUT (jobbról) – érdembeli eredmények közlésére kialakított interface
K, z_i, z_J, z_Q, z_L – közlésre kiválasztott adatok, mely tartalmazza a K elfogadott áttételi számot, valamint annak elérési útját az indexelt fogszámokkal, a kifejezés felbontás sorrendjében.
A – eredményszűrő A kritériuma: a szerelés korlátozásai, méretfüggőségek, géptípusként változik. Azért az OUTPUT után, mert ha csak ez az egy eredmény találtatik, akkor legalább tudomást szerezzünk róla. Tartóvilla korrekció igen/nem döntéshozatal lehetőséget nyújt.
KÉPERNYŐ INTRFACE – eredmények közlésének számbeli és grafikus külalakja
L : n - a folyamatértékű L index összevetése a fogaskerekek számával n = L_MAX : kisebb és egyenlő, vagy nagyobb.
L ← L + 1 – az „L” indexszámláló felveszi következő természetes szám (N) értékét.
Q : n - a folyamatértékű Q index összevetése a fogaskerekek számával n = Q_MAX : kisebb és egyenlő, vagy nagyobb.
Q ← Q + 1 – az „Q” indexszámláló felveszi a következő természetes szám (N) értékét.
J : n - a folyamatértékű J index összevetése a fogaskerekek számával n = J_MAX : kisebb és egyenlő, vagy nagyobb.
J ← J + 1 – az „J” indexszámláló felveszi a következő természetes szám (N) értékét.
i : n - a folyamatértékű i index összevetése a fogaskerekek számával n = i_MAX : kisebb és egyenlő, vagy nagyobb.
i ← i + 1 – az „i” indexszámláló felveszi a következő természetes szám (N) értékét.
OUTPUT (balról) – a kutakodás folyamatának végét kijelző interface.
STOP – a folyamat (program) vége.

4.4.) Eredményt szűrő B, C és D kritériumok folyamatábrái (lásd 2.rész c. fejezetpontját):

B.) Az „J” indexszámláló szűrőkritériumának módul algoritmusa: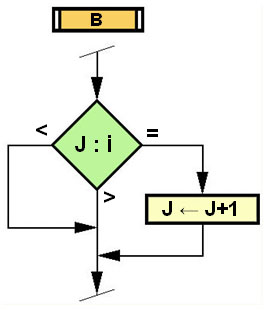

Ábra 16. : J: ha J=I akkor a rákövetkező indexértéket kel használja, azaz J→J+1.
Vázlat: LáVa























C.) Az „Q” indexszámláló szűrőkritériumának módul algoritmusa: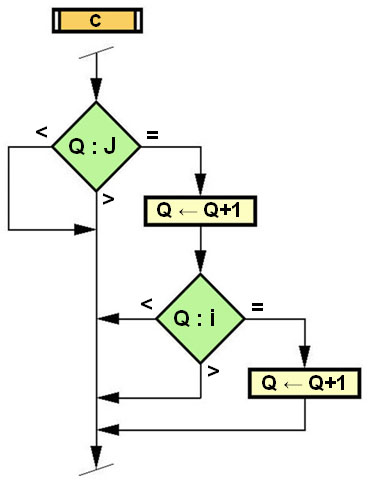

Ábra 17. : Q: ha Q=I vagy Q=J akkor úgyszintén Q→Q+1.
Vázlat: LáVa




































D.) Az „L” indexszámláló szűrőkritériumának módul algoritmusa: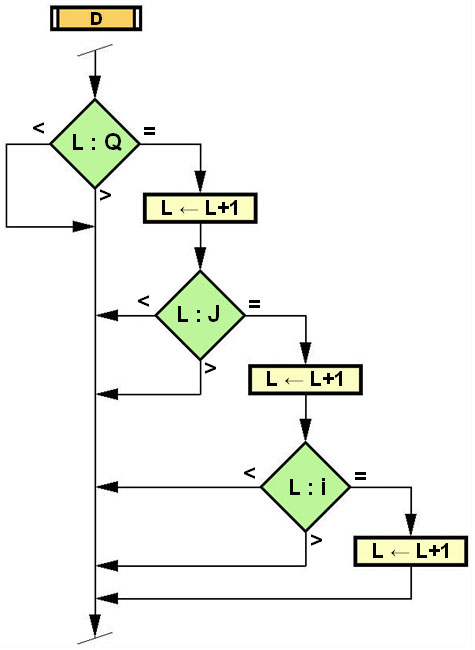


Ábra 18. : L: ha L=I vagy L=J vagy L=Q akkor L→L+1.
Vázlat: LáVa


4.4.) Megjegyzés – modellezés: A különböző művelet-összefüggések, azaz változatainak függvénye (f) és szűrő kulcsaik a számlálóban, természetes számok közt K=f(N), eredményeként léteznek különféle mintázatos és színezetű lepkeszárnyak (lásd 3. részt). Az itt feldolgozott témában ez a függvény: K=I/J*Q/L a kulcsok (többször ismételtem már idáig) láthatók a: 2. rész b), c) és d) fejezetpontjaiban.
Az alakzatuk is hasonló módon jöhet létre, de ez számomra most csak feltételes modell formájában létezhet, mert ebben a munkámban nem tértem ki a megoldást magában hordozó változó számmennyiségű indexszámokra (n≠const), azaz:

i∈[1…n₁] még összetettebben, tetszetősebb alakzatokkal i∈[1…f(n₁)]
J∈[1…n₂]                                                                                         J∈[1…f(n₂)]
Q∈[1…n₃]                                                                                         Q∈[1…f(n₃)]
L∈[1…n₄]                                                                                         L∈[1…f(n₄)]

Miközben alapértelem-szerűen: n1 ≠ n2 ≠ n3 ≠ n4 , de lehetségesek a kiegyenlítődések is, különböző kombinációkban és „ideig” (számlálás rész-szakasz lepörgéséig).

Ily módon, el lehet térni a téglalap és téglatest alakzatoktól (lásd 19. ábrát) és elasztikusan [n=f(τ)] dallamosabb alakváltozásokat produkálni, például akár fecskefarkú lepkeszárnyat is, síkban (2D) és térben (3D). Ez bizonyos esemény, kellő kikísérletezett függvénnyel és kulcsokkal, befektetett munkával.

Az igazi bizonytalan feltételezés = hipotézis az lenne, ha azt állítanám: a sejtszaporodás egy élőlény szabályos növekedésnél, tulajdonképpen egy aszimptotikusan folyamatosan csökkenő függvény mentén zajló számláló eredménye, génkulcsokkal, melyek váltsák a függvényeket és a kulcsokat. Merész feltételezés, még egyszer megismétlem HIPOTÉZIS, melynek bizonyítására és cáfolására is tervszerű kísérleteket kell végezni. Amatőr szinten semmi lehetőség sincs rá. Csak ide, oda próbálkozgatni, ami megegyezne a fogaskerék gyártástechnológus eme újítás előtti munkájával, áttételi fogaskerekek kiválasztása alkalmával, váltókészletből (lásd 1. részt, 2. fejezetét).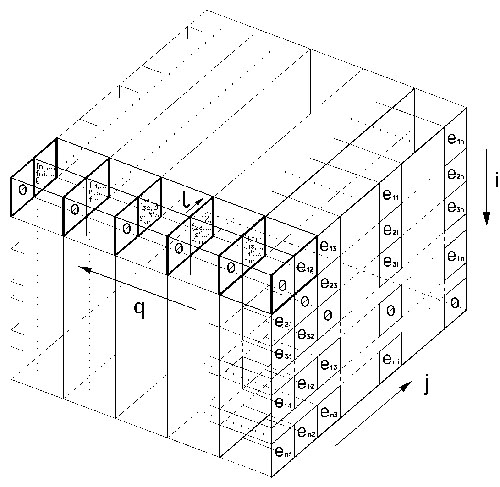


Ábra 19. : A téglatestű 4S dimenziós (négysíkú) LEPKE modell megoldástér, hamisan „4D” (négydimenziós).
Vázlat: LáVa


Ez tulajdonképpen a 2. rész gondolatszerű logikai 6. ábrája kicsikét másképpen, anyagformálóan realisztikusabban.

A csigaház megoldása jóval egyszerűbb az összes lepkeszárnytól: logaritmus spirál görbéjén, fokozatosan növekszik a kúppalást szelete, a számláló léptékeként egymásba illeszkedően. Sok mindenki ismerheti a függvény és a kúp analitikus mértani kifejezéseit. Különben, mind 3D modell megszerkeszthető a legújabb AutoCAD 2008–ban is. Majd legközelebb megteszem, de…

Ötlet(kínálat) felhívással: …inkább van egy nehezen elutasítható ajánlat javaslatom ehhez: aki „vette adásomat”, és készséget érez magában, hát, tessék, itt az alkalom: modellezze meg a (képzelt) lepkeszárnyat alakban, mintázatban és színekben. Egy okos, hasznos dologra használhatja huzamosabb időn keresztül a számítógépe (valószínűleg PC) gépidejét, és még ha közben diák is, bejelentkezhet az „Ifjúsági Bolyai Pályázat”-ra, fokozott valószínűséggel megpályázva ezzel a nem mellékes 300 000 Ft is. „Aki mer és tesz, az nyer(het)”, de semmiképpen nem veszthet. Lásd a:
http://www.fokusz.info/index.php?cid=1277750475&sid=1568912702

Egy a feltételem (!) az ötlet használatához: hivatkoznia kell a „Fókuszra” mint vajdasági ismeretterjesztő és tudományismertető portálra:
www.fokusz.info

És erre a cikksorozatra: „Fogazatos ötletelés” mind használt szakirodalomra, kezdődően az 1. részel:
http://www.fokusz.info/index.php?cid=1752456410&sid=1744601227

4.5.) A döntés: Ha összevetjük a „Fogazatos ötletelés” 2. részében, a 3.1. fejezetének, utolsó előtti bekezdésében olvasható Matematika indukció taglalását, a felkínált „Ifjúsági Bolyai Pályázat” tematikájával, megvilágosodva kitükröződik a következő közös szándékunk (lásd 20. ábrát):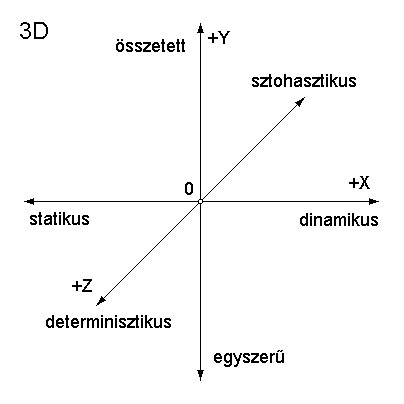


Ábra 20. : A döntéshozatal modell térábrázolása → 3D DÖNTÉS
Vázlat: LáVa


Magyarázat, könnyen érthető példázásokkal:

a.) A legkönnyebb döntéshozatal: lassan (statikus), egyszerűről, azt is nagyjából (sztohasztikus). Ez egyben a leghasznavehetetlenebb döntés is. A Descartes 3D koordinátarendszert alap-értelemszerűen ismerve, megállapítható, hogy mindhárom a negatívum irányzatokban helyezkedik, a VII. kvadránt –ban (balra, lent, hátul = -, -, -).
Ennek a „legrosszabb döntésnek” titulálható modellnek a tipikusan felismerhető megnyilvánulása az: „Ott van valahol, keresd meg”, félvállról (félálomból) lassacskán kimondott kurta válasz.

b.) A legjobb döntéshozatal: gyorsan (dinamikus), összetettről, pontosan (determinisztikus). Ehhez kell ám aztán „a legény a gáton” számítógéppel (gyorsan, sokról, pontosan), mert egyben ezt a legnehezebb megtenni, pedig a leghasznavehetőbb. Helyezkedése a koordináta rendszerből kiolvasható: I. kvadránt (jobbra, fönt, elöl = +, +, +), ahol mindegyik döntésforma pozitív irányzatú!
A döntések közismertebb formái is beazonosíthatók a felállított 3D rendszerben.

c.) Jó döntéshozatal: Ha egy jelenség (akár természeti, vagy fogalmi) viszonylag betekinthetően egyszerű (változóan kinek-hogy?), közismerten aránylag gyorsan és pontosan dönthetünk róla. Ez az V. kvadránt (jobbra, lent, elöl = +, -, +), ahol gyorsan (dinamikus), egyszerűről, pontos (determinisztikus) döntések jönnek létre.

d.) Kapkodó döntés: erről is már hallott mindenki, esetleg része is volt benne. Tartalmilag teljesen meghatározható: a jelenségek sokasodnak (összetett), az idő kevés (dinamikus) és a pontosságnak egyszer csak lőttek (sztohasztikus)! Helyezkedése a II. kvadránt (jobbra, fönt, hátul = +, +, -). Ilyenkor szokott elhangzani: „Édes fiam – lányom, ne kapkodjá’ má’ !?”, a nem jól eső figyelmeztetés. Mi a teendő ilyenkor?

Mint mindig is az esetek túlnyomórészében, a válasz egyszerű, és a „földön, előttünk hever”…

…Folytatása következik…