Fogazatos ötletelés: a program

1. rész
2. rész
3. rész
4. rész
5. rész
6. rész

Előzetes: Ki gondolta volna, hogy az aránylag rövid időrendekben sorakozó, egymásutánban bevillanó ötleteket, amelyeket valamelyest hosszabb ritmusokban fel is tudtam magánjellegűen építőszerűen dolgozni, miáltal létrehoztam a bemutatás alatt lévő innovációt – elfogadott hasznos javaslatot, tovább tart majdnem ismertető prezentációként kidolgozni, mint kigondolni. Én sem. Így, előttünk van már a harmincharmadik (33.) oldalán, a hetedik (7.) folytatás, a 4.6.) A PROGRAM fejezet, következő alfejezete:

4.6.2.6.) SZÁMÍTÁS MAG – KERNAL: (lásd 24a. ábrát) Összefoglalva a 391. és 575. kódsorok között, egymásba ágyazva tartalmazza a központi indexes számláló hurkait. A: FOR TO STEP NEXT számlálókat, IF THEN ELSE szűrőket és a K=… műveletet, egymáskövető formában:

a.) Az első, külső hurok, „I” index számlálója a 410. kódsor, tartományszűrője a 415., indexnövelője és visszatérítője (a 410.-re) az 570. kódsor. Nyilvánvalóan, mint az 1000km számlálója, magába foglalja a 100, 10 és 1km is, vagyis a „J”, „Q” és „L” változó indexeket. Az algoritmusonez szemléletesen érzékelhető (lásd 5. rész, 15. ábráját).

b.) Következik a második „J” hurok, akár egy második tojáshéj, az elsőn – külsőn belül. Számlálója a 420. és 560. kódsor, kulcs szűrője a 430. sor (lásd B algoritmus modult, 5. rész, 16. ábra), érvényességének tartomány szűrője a 435. sor (egyáltalán a keresett K értéke bele esik e a pillanatnyilag számlálásra befogott tartományba).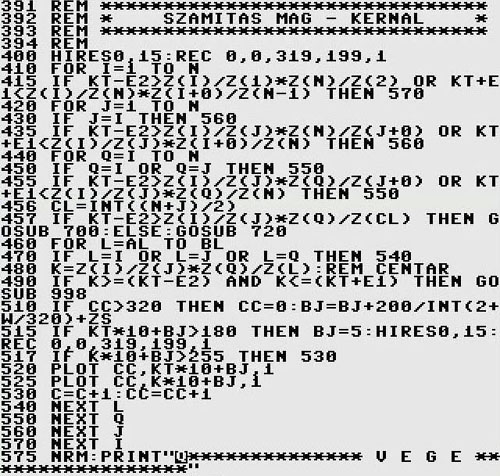


Ábra 24a. : A Programmag - KERNÁL kódsorai, az egymásba ágyazott „I”, „J”, „Q” és „L” indexszámláló összefoglaló hurkaival.
Programozó: LáVa

c.) A „Q” számláló hurkot a 440. és 550. kódsorok és köztiek foglalják magukba. Itt is van kulcsszűrő, a 450. kódsor (lásd C modult, 5. rész, 17. ábra) és tartományszűrő a 455. sor.

Ha azt gondoltam volna, már minden meg van oldva, csak kódolt programsorokká kell formálnom a modellt, tévedtem. Figyelmem a próbafuttatások során, egy monoton kitérésű, célt tévesztő „golyószórózó” jelenség vonta magára. Ezért, most a lineárisan sorról, sorra való program bemutatást átváltom logikai sorrendé. Így, érthetőek lesznek az elsőre elütő, előzménynélküli kódsorok, a 456., 457. és 460.-ik. Úgyszintén, belopakodott a számlálásra pillanatnyilag befogott tartomány fogalma is (415., 435., 455. kódsorok). Ezek és az előzőek is a számláló üresbe „pufogtatást” hivatottak kikerülni, ahogyan az elején a Kmin és Kmax értékeinek kiszámítása és összehasonlítása a keresett Ko-val is.


Az 510. – 530. kódsorok tartalmazzák a legbelső „L” hurkon belül a számlálás folyamatát képernyőre kivetítő grafikus ábrázolását (ciklusoknak is nevezhetők). Ez állandó jellegű és roppant szemléletes: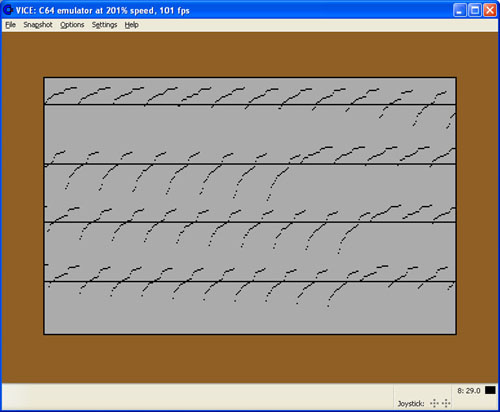


Ábra 24b. : A képernyőn grafikusan követhető a számlálás folyamata. A vonal képezi a keresett Ko áttételi számot, amelyet „golyószóró” módban indexsorozatokkal átpásztáz a számláló. A ”J”, „L” és „Q” indexpergések jól kivehetők a képernyőről lementett képről (Print Screen).
Programozó: LáVa

Érdekességként: beazonosítható a modell „LEKPE” egy zöld négyzete (lásd 3. rész, 9a ábráját), egy raszter (pontszerű) vonalkával a fenti képernyőről, ahol bármely vonalka alsó első pontja az L=1 indexérték (vagy az első engedélyezett), a fölső pedig logikaszerűen L=N=29, ebben a PA váltófogaskerék-készlet példában.

Leolvasható a fenti 24b. ábráról - képről, hogy az „L” indexvonalkák valóban egymás utáni folyamatos monotonsággal megsüppednek és megnyúlnak, követve a „Q” indexszámláló pergő növekedését, és mely egy „J” indexszámláló értékén belül behatárolható „ferde” tömbhalmazt alkot. Egy „I” indexváltás nem fér el egy képernyőn. Jellemző rá a számláló harmonikusan hullámzó monotóniájának szakadásszerű ugróváltozása, lentről, fel, ismét jellegzetesen jóval rövidebb „L” indexvonalkákkal (hasonlóan, mint az ábrán a „J” indexváltások).

Egy megjelölésekkel kiegészített 24b. ábra ezt teljesen érthetővé teszi vizuálisan is (lásd 24c. ábrát):


Ábra 24c. : A kiosztott „I”, „J”, „Q” és „L” indexszámlálók megjelölésével, vizuálisan is számon követhetők változásaik a grafikus interface-n.
Programozó: LáVa

Innen, a képről ered az ötlet a megfelelő eredmények precízebb megcélozásához. Minek az a sok „golyószórószerű” számoltatás, mikor a kitűzött célvonal Ko érintéséhez szemmell láthatóan az „L” pontvonalkák hosszából a felinek, a felinek a fele sem kell! Matematikailag ez a szójáték egyértelműen nyolcad részt jelent: ½ * ½ * ½ = 1/8. A kérdés csak az: melyik az a nyolcad, amelyben megbújhat a tűrésmezőbe eső Ko:
Ko-e2 < Ko < Ko+e1

határai között? Valójában ez nem találós kérdés. Az „L” hurkon belül egy újonnan bevezetett tartomány mező kulcs képezi, a már megemlített 456., 457. és 460. kódsorok IF THEN ELSE

( = ha akkor ellenben) válaszútjai. Működésüknek filozófiája szemléletesen látszik a következő, 24d. ábrán: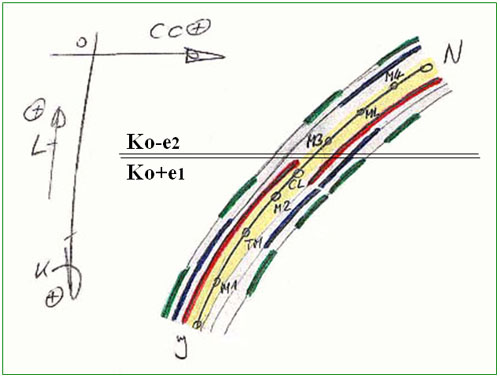


Ábra 25. : Az eredeti kézirat „L” J-N sárga indexvonalka tartományán belüli mező kulcsok:
felek (1/2): J-CL és Cl-N
negyedek (1/4): J-TM és TM-CL, vagy CL-ML és ML-N
nyolcadok (1/8): J-M1 és M1-TM, vagy TM-M2 és M2-CL,
valamint: CL-M3 és M3-ML, vagy ML-M4 és M4-N.
Programozó: LáVa

Eredményes számláló (= lapozó) kutakodást a 25. ábrán, csak a CL-M3 1/8 mező tartományában érdemes végezni. Tehát mindig csak az ”L” vonalacska 1/8. Ezzel a program kutakodásának gépi ideje körül-belül 87,5% -al csökken! És számít ez valamit a mai gyors (számító) gépeknél? Határozott IGEN (és van, akiknek nem), mert:

A PA egyetemes esztergapad váltófogaskerék-készletét n=29 fogaskerék képezi. A felinek, a felinek, a felét 3-4 fogaskerék képezi, Ko eliminációs összehasonlításokkal kiválasztott nyolcadából (1/8). Gépészetről lévén szó, a szép új autókat különben is tömegében kedvelik az emberek, a gyártás fogalmát sem lehet megkerülni. Az említett járgányokat túlnyomórészt nagy sorozatokban, sőt egyes alkatrészeit tömeggyártásban állítják elő. És itt minden számít. Főleg minden töredék időrész, ez a gyártás filozófia. Mennyire valós ez, példázom egy T=0,1sec/db megtakarítással egy gyártmánytechnológián, 1 000 000 (millió) darabszám előállításánál (kb. egy havi termelés). Összesen 100 000 (százezer) másodperc (sec) megtakarítást „hoz a konyhára”:

(100 000sec : 3600sec/óra) : 16óra/nap (két váltás) = 1,7361 munkanap megtakarítás!!
Vagyis, valamivel több, mint három (3) váltást takarítanák meg egy hónapon belül. Mit jelent ez megfoghatóan? Nagyon meg lennék elégedve keresetemmel, ha „csak” ezt a megtakarított idő pénzértékét kapnám kézhez, vagy felét. Úgyszintén nagyon nem voltam megelégedve, és továbbálltam, mikor 100% (500 000 → 1 000 000) megtakarításért 0+ értéket kaptam, és már nem először. Akár a mesékben, mikor a „szegény ember harmadik fia” is fogta tarisznyáját, vádrobotját és bízva önmagában „világgá ment” (máshova) szerencsét próbálni (megalkotni). Meg is tette és meg is találja.

…Folytatása következik…